R-L-Cと電圧/電流の関係性：単相交流回路で満点を取る３ポイント

直流と交流

多少交流についても学びますが、高校物理までで学習するのは基本的に直流です。直流は時間により向きの変化が変化しない電気の流れのことです。現場ではDC（Direct Current）と呼びます。これに対して、交流は時間によって大きさや向きが周期的に変化する電気の流れです。現場ではAC（Alternating Current）と呼びます。ここでは、まず基本形である下図１のような正弦波交流を理解しましょう。

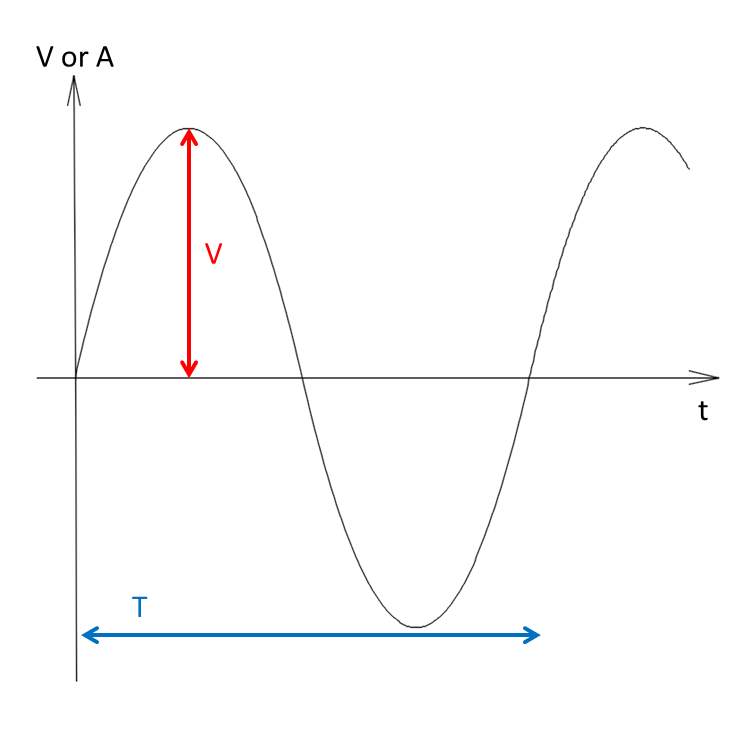
山１つ、谷１つが１セットです。１セット電気が変化するのにかかる時間を（　①　）\(T\) [s] と言います。また、１秒間に何回山と谷が変化するかを（　②　）\( f \)と言い、 単位は（　③　）を用います。この\(f\)と\(T\)の間には（　④　）の関係式が成り立ちます。定義のままですから、敢えて「覚える」ほどのものでもないですけど。さらに角速度を\(\omega\) [rad/s] とすると、\(f\)との間に（　⑤　）の関係性が成り立ちます。

最大値と平均値、実効値の関係

先ほどと同様に正弦波交流の電圧について考えます（電流でも全く同じです）。振幅と呼ばれる正弦波の幅が基準になります。これを正弦波交流の最大値\(V\)とします。この\(V\)を用いて正弦波交流の平均値\(V_{av}\)は（　⑥　）と表せます。また、実効値\(V_m\)は（　⑦　）と表せます。実効値とは、直流と同じ（　⑧　）を消費する値のことを言います。交流は時々刻々と向きや大きさが変化していますので、把握するのが難しいのです。この交流を直流と同様に扱えるようにしたのが実効値です。電験の問題でも特に断りが無い場合には実効値を考えています。

R-L-Cが電圧と電流に与える影響

抵抗R、リアクタンスL、コンデンサＣが電気の流れに及ぼす影響を見てみましょう。個々の詳しい解説は後日行います。考えるべき要素は電流と電圧にどのような位相差が生じるかです。簡単にまとめると、次のようになります。

　抵抗R →　\(\dot{I}\)は\(\dot{V}\)に対して（　⑧　）

　リアクタンスL　→　 \(\dot{I}\)は\(\dot{V}\)に対して（　⑨　）

　 コンデンサC　→　\(\dot{I}\)は\(\dot{V}\)に対して（　⑩　）

---

交流回路の問題は、①ベクトル図を描く、②複素数計算をする、の２通りの考え方があります。計算は面倒なものの、最終的には②で全ての問題が解けるのですが、実際の試験では時間制限もあるので、①のベクトル図を描く解法も必要に応じて使えるようにしておかなければなりません。ここから先の解説では、複数の解法が考えられる場合には、どちらの解法も合わせて紹介します。そして、どちらか一方でしか解けない場合には、その理由も合わせて解説します。

よく勘違いしている方がいらっしゃるのですが、交流回路でも、直流回路と同様に、「キルヒホッフの法則」や「オームの法則」は成り立ちます。上手くいかないのはベクトル計算や複素数計算の意味が正しく分かっていないことが原因だと思われます。後ほど紹介する実践問題でご確認ください。

【直列回路】R-L-Cが電圧と電流に与える影響

下図２のような直列回路を考えようと思います。

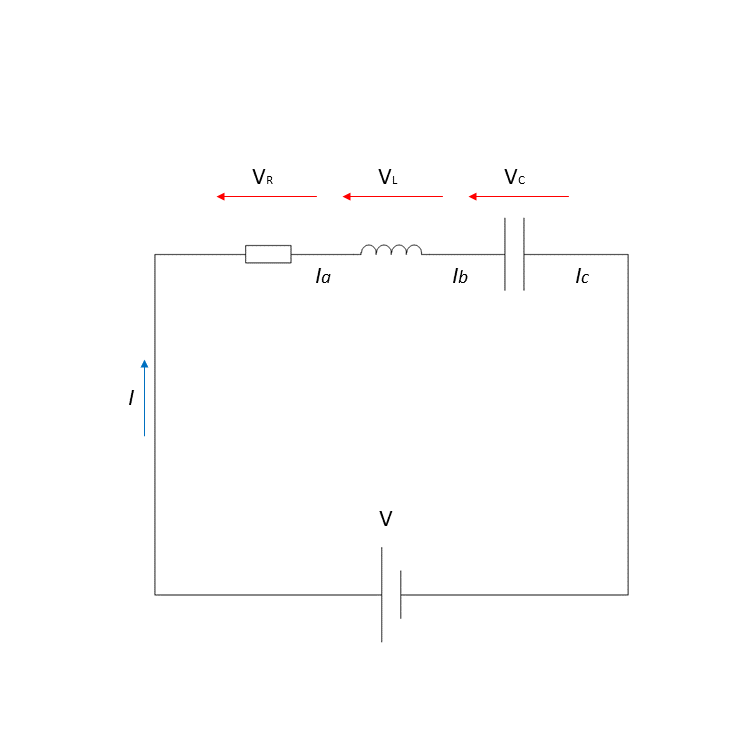
電圧 \( \dot{V} = \dot{V_R} + \dot{V_L} + \dot{V_C} \) 、電流 \( \dot{I} = \dot{I_a} = \dot{I_b} = \dot{I_c} \) の関係式が成立しています。直流と基本的な考え方は同じです。交流ではベクトルになっていることに注意をしましょう。ベクトル図は、位相が変化しない電流 \(\dot{I}\) を基準にして描くことがポイントです。

ちなみに、複素数でインピーダンス \( Z \)を表すと、\( Z = R + j X_L + \displaystyle\frac{1}{jX_C} \) となります。

【並列回路】R-L-Cが電圧と電流に与える影響

次は、下図３のような並列回路を考えようと思います。

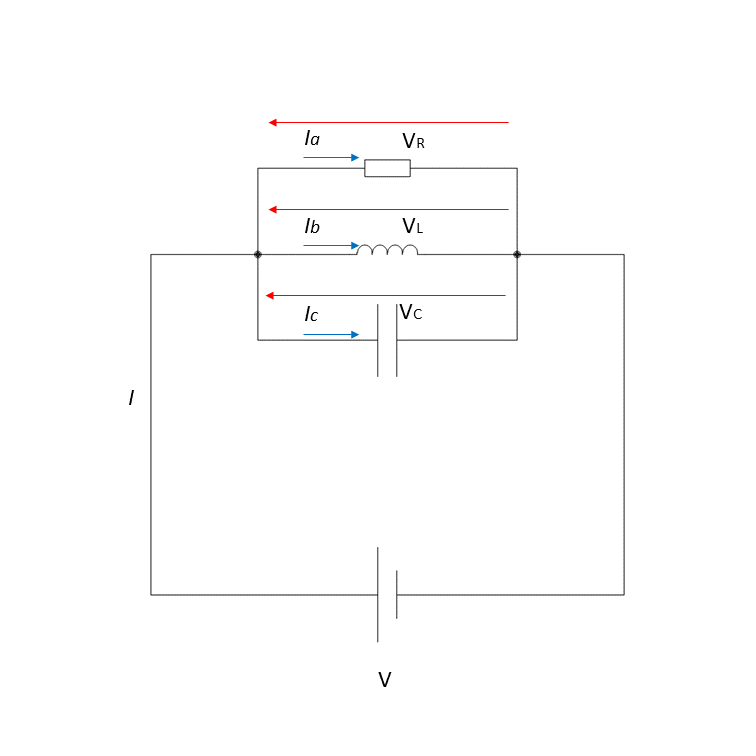
電圧 \( \dot{V} = \dot{V_R} = \dot{V_L} = \dot{V_C} \) 、電流 \( \dot{I} = \dot{I_a} + \dot{I_b} + \dot{I_c} \) の関係式が成立しています。これも直流と基本的な考え方は同じです。交流ではベクトルになっていることに注意をしましょう。ベクトル図は、位相が変化しない電圧 \(\dot{V}\) を基準にして描くことがポイントです。

ちなみに、複素数でインピーダンス \( Z \)を表すと、\( \frac{1}{\;Z\;} = \frac{1}{\;R\;} + \frac{1}{j X_L} + \displaystyle\frac{1}{\frac{1}{j X_C}} \) となります。この分数式の取り扱いが面倒なので、より計算しやすくするためにアドミタンス（インピーダンスの逆数）を用いることがあります。実際の問題で使い方を見た方が分かりやすいので、ここでの説明は割愛します。

交流の電力

直流の電力は\(P=IV\)で良かったのですが、交流は先述したように「位相」が絡んでくるのでやっかいです。電圧と電流が同相にになる部分しか有効な電力とは言えません。そこで、下図４のように３つの電力を考える必要があります。

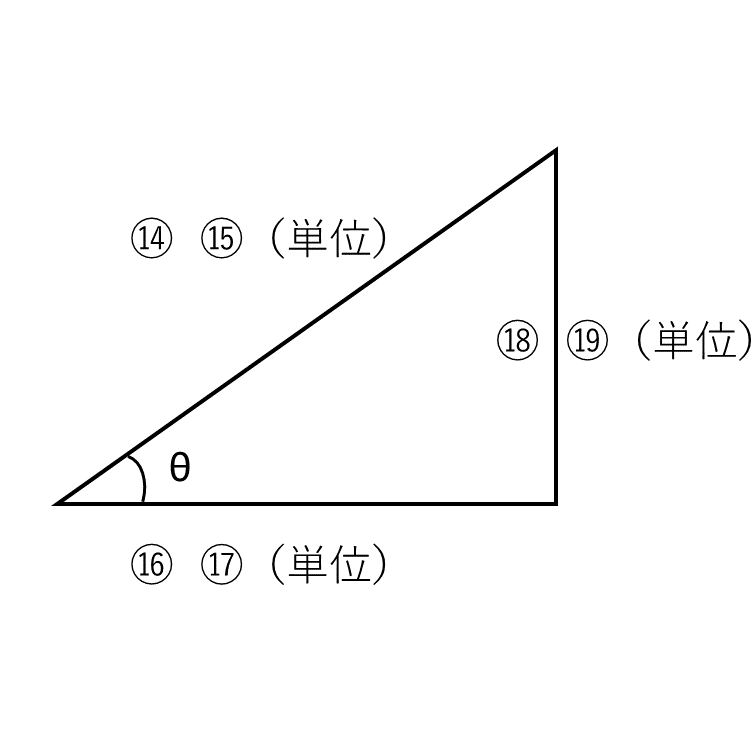
\(\theta\) の角度が分かっていれば、３辺のうちのいずれか１辺の大きさが分かれば、あとは三角比で他の辺（電力）の大きさも分かります。（　⑭　）に対する（　⑯　）の割合を（　⑳　）と言います。電気料金にも大きく関わるので、現場でも必ず計測する重要な値です。-１～０（-１００％～０％）を進み（Lead）、０～＋１（０％～＋１００％）を遅れ（Lag）として表記します。図で表す場合には、反時計回りを「遅れ」、時計回りを「進み」として表記するのが一般的です。

話を元に戻します。\( P = \)（　㉑　）と表すことができます。

共振現象

交流回路においてリアクタンスやコンデンサがあれば電圧と電流の位相の間にはズレが発生します。しかし、（　㉒　）の条件を満たすことで、電圧と電流の位相のずれが無くなります。この現象を共振現象と呼びます。この時の周波数 \( f_0 \) を（　㉓　）と呼びます。\( f_0 = \frac{1}{2\pi\sqrt{LC}} \)の条件が成立しますが、この条件を覚える必要性は特にありません。㉒を変形すればこれが導き出せるからです。無駄なことは覚えずに、効率的に電験を突破しましょう！

おまけ：非正弦波交流

後日追記します。今しばらくお待ちください。

確認問題：平成２３年理論A問題　問８

後日追記します。今しばらくお待ちください。